Disassembling Carnatic Parental Scales Programmatically - Part 3
Disclaimer:
My goal is to share the journey I took in deciphering and printing all the 72 Parental scales of South Indian classical music. I am intentionally avoiding notations Ri1, Ri2, Ga2, Ga3 as it was only adding confusion and complicating the programming aspect. So for simplicity, I am sticking to western notations. Only sharps (#), no flats either.
I sincerely respect everyone's sentimental values they hold with regards to the classical music (So do I). But I humbly request all purists and pundits to look elsewhere if you feel offended that I am muddying the waters or adding impurity to the tradition. May be I am doing both.
If you are not into computer programming, this may not serve much. My aim is to share my findings with like minded people who have a common interest in understanding music theory by writing some simple code.

Hemanatha Bhagavathar
Continuing on the same methodology as in my previous article where I explained how to print the major and minor scales of the western classical music, I ventured on to the 72 Parental scales of South Indian classical music. And in the same lines, I have written yet another C program exclusively to print all the 72 scales with their Arohanams and Avarohanams.
Just like how there is a formula for major scales (2+2+1+2+2+2+1) and a formula for minor Scales (2+1+2+2+1+2+2), there are 72 unique formulas in total, one for each scale of South Indian classical music. These 72 parental scales are collectively known as “Melakarta Ragas”. And whatever I am calling here as formulas, in musical literature apparently they are called as the “key signatures” I.e., One Key signature per Scale.
The reason being called as parent scales is because from each of these 72 scales, we can derive many child/children scales (aka, Janya Ragas) There is a set of guidance that is being provided as to how to go about deriving child scales. As long as we implement as per the guidance, nothing is preventing us in creating one of our own. I am hoping to write a separate article on its logic. For now, the closest analogy we can think of is how we do “subnet masking” in networking. More on it on a later article.
Though I use terms Scale and Raga interchangably, I am learning that they are not exactly one and the same. So I will try to stick to the term 'Scales' and use the term 'Raga' only when needed.
For any beginner, the terms - Scale, Raga, Swaram, Swarasthanam, Arohanam, Avarohanam are quite intimidating. So I have explained the way I see it, with my own anology. An anology that we all are quite familiar with. Once you draw parallells to this anology, I promise everything around those terms will fall in place.
Before proceeding any further with this article, I would strong recommend you watching all my videos using specific analogies in PART 2 as they will give you some bearings in understanding the theory better.
In this part of the article, I will primarily focus on everything that we need to understand in constructing a C program to print all the 72 scales. In the following parts, I will cover more in-depth on key signatures. And I guarantee you that you will be fascinated in seeing some simple + beautiful patterns emerge when you put all key signatures together.
I am breaking up this article into multiple stages in piecing up all the puzzles:
Stage 01: Source of truth that I followed to understand the anatomy of all 72 parental scales
Stage 02: Assimilating the data provided at the source and mapped with western notations
Stage 03: Deciphering the formula (key signature) for any given scale
Stage 04: Assembling the key signatures of all the scales into a double dimensional array
Stage 05: Retrofitting all arrays into C program for printing all the scales
Stage 01: Source of Truth
Though Wikipedia has a ton of information, most of it went over my head. But there is just one brilliant website that has everything beautifully captured. In fact, it is this website that kindled my curiosity and spirit and made me dig indepth. And here it is:
It has just one big beautiful circle right in the center with navigation controls on the side. This is my only source of truth that I referred to. ( I now notice that they have recently introduced a new link to give the mappings between classical notation and western notation which wasn't there before. So I had to do the mapping part myself manually)
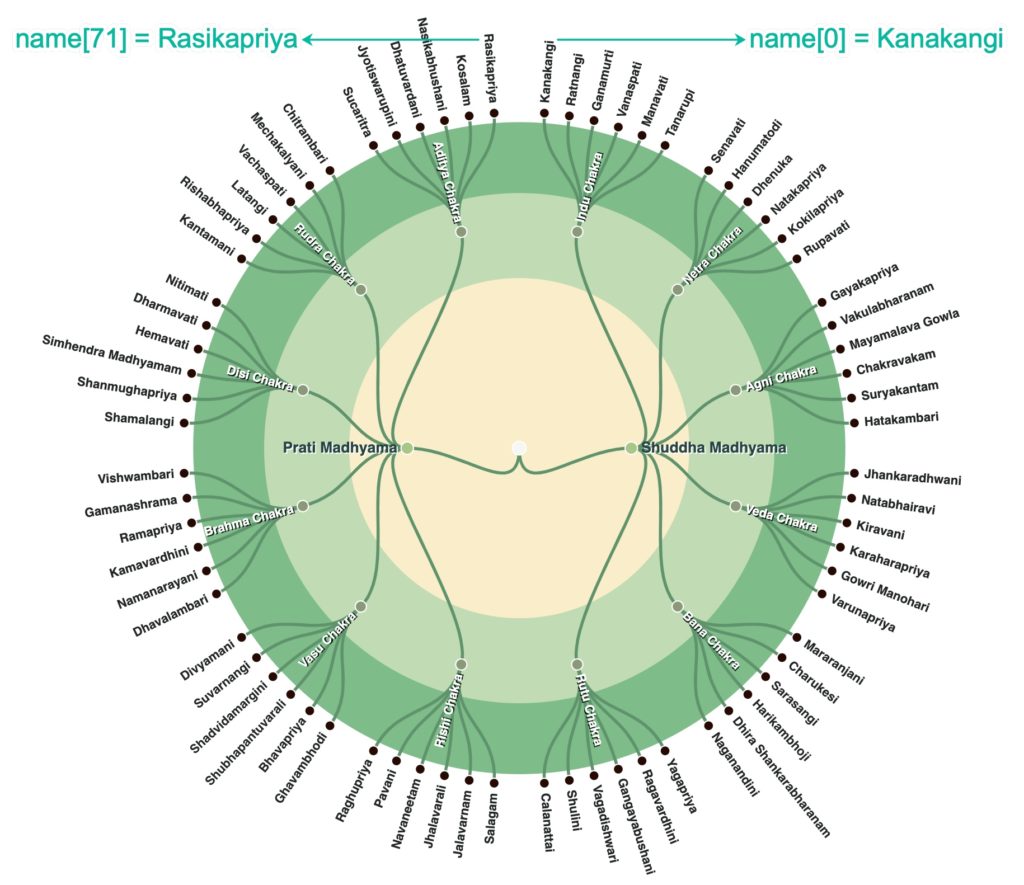
Credits: www.melakarta.com
When you take one close look at it, there are so many ways we can represent the above data - circular linked lists, double dimensional arrays to multiple single dimensional arrays. I chose to go with double dimensional arrays as that would suffice our programming needs.
Stage 02: Mapping Carnatic notation to Western notation
Let us take the very first scale - Kanakangi on the top. We need to go clockwise and end at Rasikapriya. As you can see there are 12 chakras and each one of them hold 6 scales. Whe we click on any scale, we will get a popup window with it's details. And there lies its key signature! (Note: You need to try that at melakarta.com website and not on the above image).
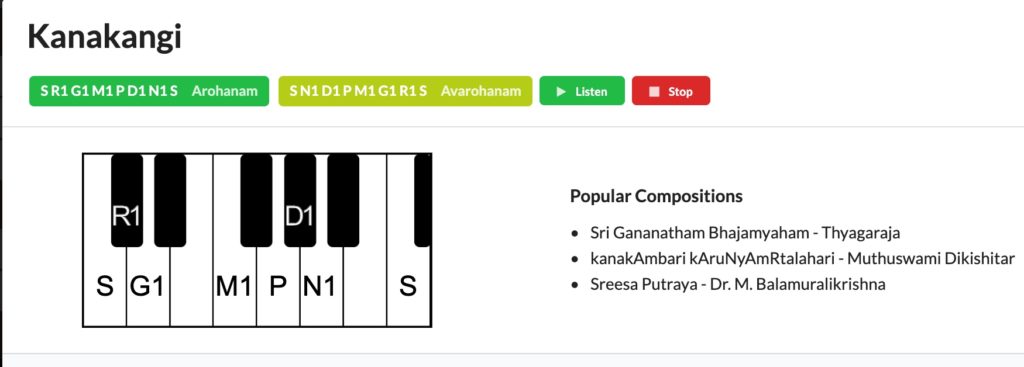
Credits: www.melakarta.com
Now let us superimpose the western notations on them and see how it looks:
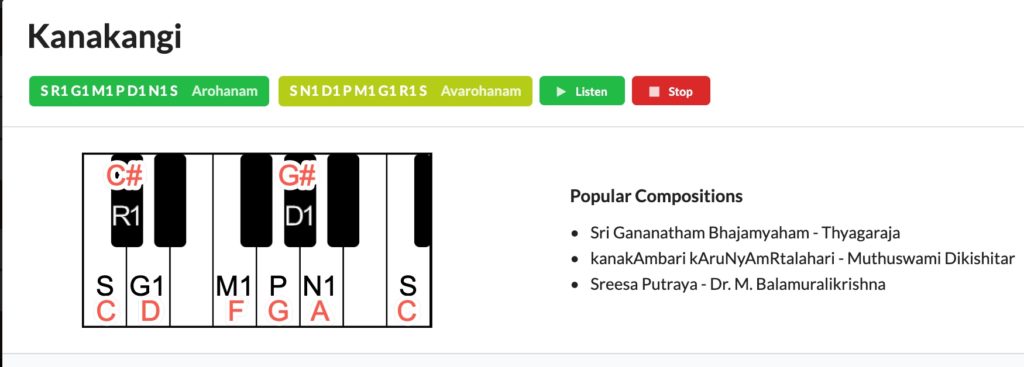
Credits: www.melakarta.com
What it means is that - to play the scale Kanakangi:
We start from the very first white key of the Octave, play ONE AND ONLY those notes that are marked and skip the rest. We will be commiting a crime (so I am told) if we dare to play any other keys and still call it Kanakangi. That is one big NO NO. We might play a different note (intentionally or unintentionlly) and that might turn into a valid scale in by itself but it CANNOT be called Kanakangi, period. Only those notes marked above alone make up the scale Kanakangi.
a) Soon we will put them in an array and traverse from left to right (called Arohanam)
b) We will then traverse the same array in reverse as well (called Avarohanam)
c) We can think of Avarohanam as a stack operation (LIFO - Last In First Out)
d) You will see a temp array named reverse[] in the C program just for that purpose
e) All of this will be clear once you see the output of the program - 72-Scales.out
Stage 03: Deciphering the Golden Rules (Key Signaures) for scales Kanakangi and Rathnangi
I started with scale Kanakangi and went all the way to Rasikapriya (refer the Big circle above), each time figuring out it's numerical formula that is needed for the C program. To keep it simple, let us zoon in only the first two scales namely Kananagi and Rathnangi. Let us go ahead and compare the keyboard format and its array format for a couple of scales side by side:
In my previous article, I have explained in detail, the reasoning and the mechanics of using arrays and its traveral opeations. So I will skip the explanation part this time.

Programmer's view for scale Kanakangi in an array:
PRINT: key[0] , key[1] , key[2] , key[5] , key[7] , key[8] , key[9] , key[12]

Musician's view for scale Kanakangi on a musical keyboard:
PLAY: Half note + Half note + Whole & Half note + Whole note + Half note + Half note + Whole & Half note
Programmer's view for scale Kanakangi in an array:
int signature[0][7] = { 1, 1, 3, 2, 1, 1, 3 } ;
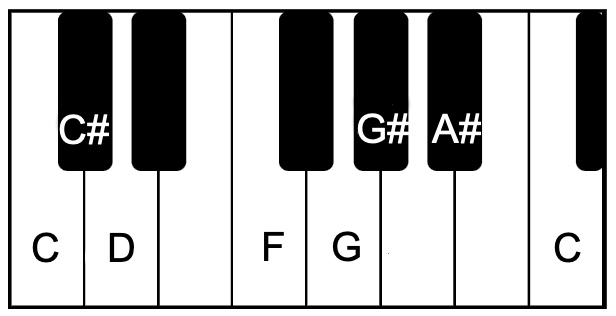
Programmer's view for scale Rathnangi in an array:
PRINT: key[0] , key[1] , key[2] , key[5] , key[7] , key[8] , key[10] , key[12]
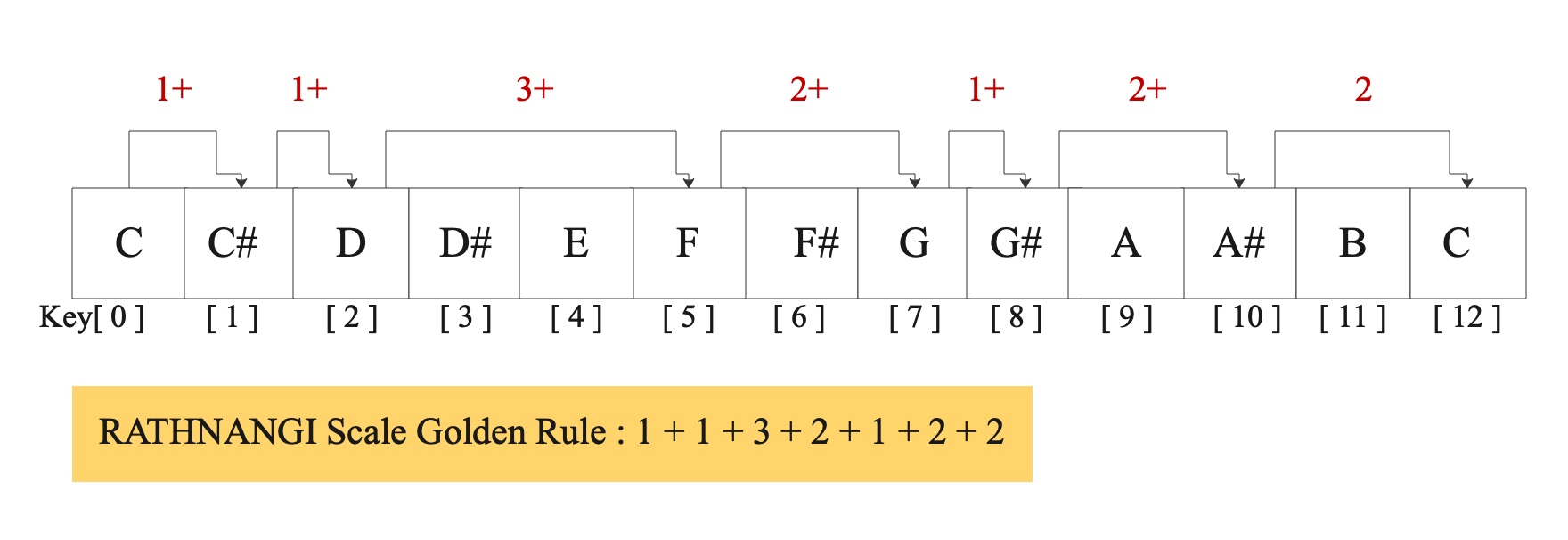
Musician's view for scale Rathnangi on a musical keyboard:
PLAY: Half note + Half note + Whole & Half note + Whole note + Half note + Whole note + Whole note
Programmer's view for scale Rathnangi in an array:
int signature[1][7] = { 1, 1, 3, 2, 1, 2, 2 } ;
As you can see what we have derived are the golder rules (ie, the Key Signatures) for the scale Kanakangi ( 1 + 1 + 3 + 2 + 1 + 1 + 3 ) and for the scale Rathnangi ( 1 + 1 + 3 + 2 + 1 + 2 + 2 ) . Now that we are done with the first two scales, let us do one by one for the rest of 70 scales right now (?!). Just kidding 🙂 I have painstakingly completed that part as well. So will save some time here.
Let us Summarize:
A scale is a generic term that denotes a collection of UNIQUE COMBINATIONS OF KEYS/NOTES known as a KEY SIGNATURE. The name given to a scale is just a reference to it. In simple terms - the name is just a label given to a unique key signature. There are 72 unique key signatures. And so there are 72 names (from Kanakangi to Rasikapriya).
Stage 04: Key Signatures in a double dimensional array
Let us go ahead and create a double dimensional array signature[][] to store all of the 72 golden rules (key signatures) one for each scale. I have done my level best to write clear comments so that it can be self-explanatory (hope so).
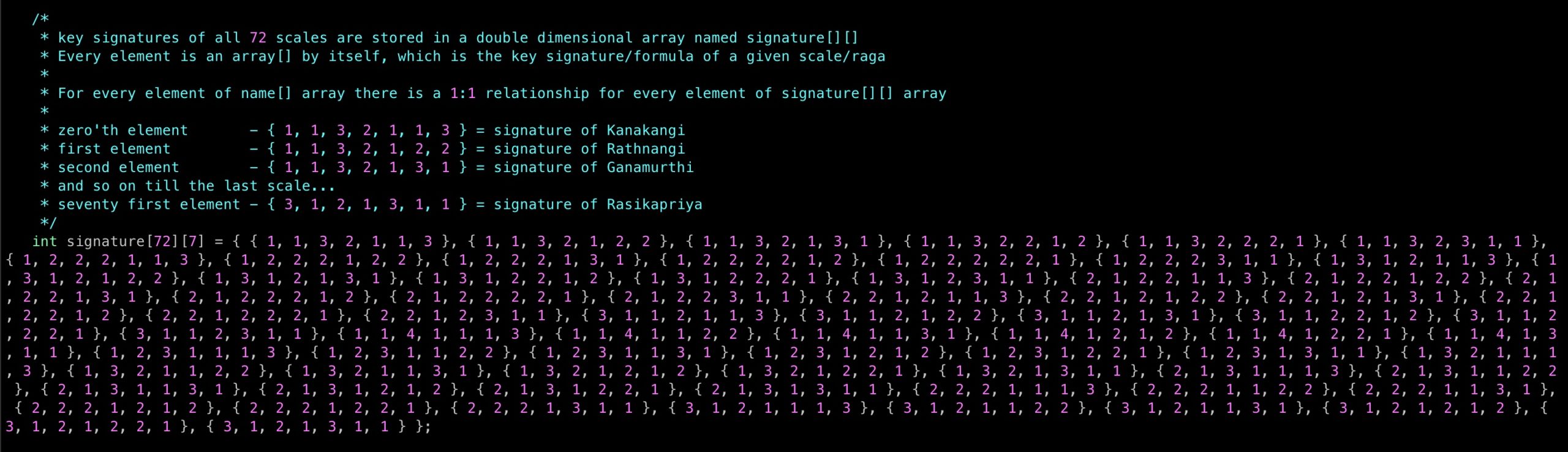
Stage 05: Bringing them all together
Now that the hardest part of deciphering the key signatures of all the 72 scales are done and dusted, let us assemble a few more arrays. One key[] array to store all the 12 (+1) keys within an Octave in the musical keyboard:

And name[] array to store names of all 72 scales:

Let us define a few variables to use them for loops, an array named temp[] to store the key signature of a given scale temporarily and an array named reverse[] to print the scale in the reverse order (Avarohanam).

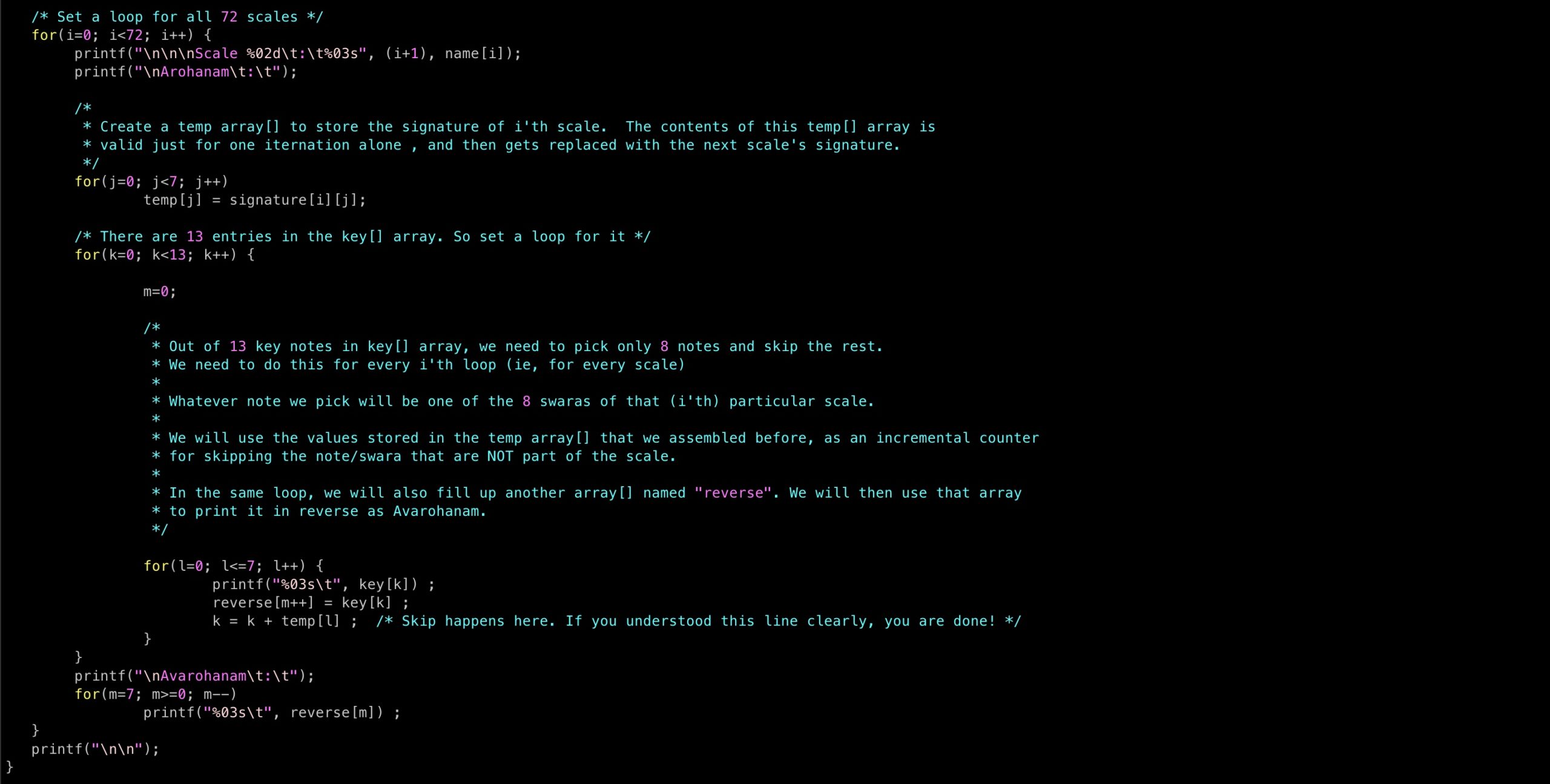
And finally the rest of the code:
- For each element in the array name[]
- Pick its corresponding entry from the double dimensional array signature[][]
- Assemble the contents of temp[] array from the above signature[][]
- Start printing every element of array named key[] , use the contents of array temp[] to skip the elements that are not part of the scale
- As the elements are printed , store the same elements in the array reverse[]
- At the end of the loop, print the contents on the array reverse[] in the reverse order, calling it Avarohanam
- Repeat all the above steps for every element in the array name[]
- You're done!
Downloadables:
Here is the Source program and the Output file. I would strong encorage you to download the source, compile it, run it and see it for yourself. Also, please feel free to share them, pass it around if needed. You can claim them as all yours and I woudn't know 🙂
Next Steps:
People who want to learn (or their kids to learn) all 72 scales and get a feel for it, but not too keen on understanding any more technical details, this article is sufficient enough and is a good stopping point. For the rest of the curious minds, check PART 4, PART 5 and PART 6 where I continue the journey.
Best wishes,
Hemanatha Bhagavathar